Conservation laws and flows in porous media
The group works with conservation laws, especially when applied to multiphase flow in porous media. We deal with research and development of accurate numerical methods and software for flow simulators in petroleum reservoirs, which may be used in oil recovery optimization. The multiphase flow models have non-trivial mathematical difficulties, represented by partial differential equations of elliptic-hyperbolic type. The solution of elliptic-hyperbolic conservation laws is important not only for oil, but also for other areas such as elastoplasticity and magnetohydrodynamics.
Oil recovery in pre-salt areas
One of the difficulties to the recovery of oil in Brazilian pre-salt layer oil fields is the great heterogeneity of the rock. The heterogeneity reduces the efficiency of conventional methods, since a large portion of the oil reservoir is located in places with low permeability and cannot be recovered. In this study we propose to study the method in which pressurized air is injected into the light oil deposit and reacts with part of it, generating heat. The heated oil evaporates from low permeability regions and condenses in regions with high permeability where it can be later retrieved.
Thermal Oil Recovery in Mature Fields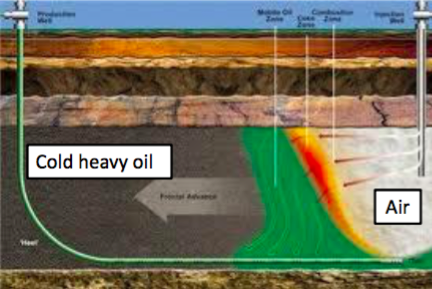
Mathematical methods are developed to research "Tertiary Recovery" in mature fields in production decline phase (case of offshore fields in the State of Rio de Janeiro). A multidisciplinary approach, based on Applied Mathematics combined with Modeling and Computer Simulation is being developed for theoretical and numerical investigation of the enhanced recovery of hydrocarbons in heterogeneous oilfields at multiple scales; the remediation processes of groundwater and soil contaminated with non-aqueous liquid phase; and reduction, containment and control of carbon dioxide levels in the environment.
Waves and droplets
 Research in this area includes the study of propagation of water waves, sound waves and atmospheric waves. In the first and last cases, the heterogeneous medium consists of the topography. For acoustic waves, the earth crust is modeled as a heterogeneous laminate medium, ie with varying properties. When the medium is messy probability theory is used to characterize the transmitted and reflected waves. From a mathematical point of view, the tools are theory of partial differential equations, asymptotic analysis and scientific computing. With respect to the numerical modeling, various methods are used depending on the application: finite difference contour elements or finite elements.
Research in this area includes the study of propagation of water waves, sound waves and atmospheric waves. In the first and last cases, the heterogeneous medium consists of the topography. For acoustic waves, the earth crust is modeled as a heterogeneous laminate medium, ie with varying properties. When the medium is messy probability theory is used to characterize the transmitted and reflected waves. From a mathematical point of view, the tools are theory of partial differential equations, asymptotic analysis and scientific computing. With respect to the numerical modeling, various methods are used depending on the application: finite difference contour elements or finite elements.
Advances in this issue concern leaping drops in vibrating containers. The problem related to Faraday instability deals with a drop guided by its pilot wave, a problem which refers to quantum mechanics in the form of the famous wave-particle duality. In a confined region in which the container has large vertical acceleration, the pilot wave moves in a medium with large propagation velocity variability behaving like a heterogeneous environment. Several questions about the predictability of the drop position are open and draw a parallel between classical mechanics and quantum mechanics. The methodology for this research combines laboratory experiments, made by the group at MIT, with mathematical modeling and scientific computing developed at IMPA.
Hydrodynamic turbulence
 Existence of singularities formed in finite time (blow-up) in incompressible flows is a long-standing open problem in mathematics. Such singularities can be an efficient mechanism of energy dissipation, as predicted phenomenologically by Kolmogorov and Onsager. A similar problem for the Navier-Stokes equations is selected as one of the Millennium problems.
Existence of singularities formed in finite time (blow-up) in incompressible flows is a long-standing open problem in mathematics. Such singularities can be an efficient mechanism of energy dissipation, as predicted phenomenologically by Kolmogorov and Onsager. A similar problem for the Navier-Stokes equations is selected as one of the Millennium problems.
Not yet available is a rational formulation of turbulence, which deduces the observed behavior of turbulent flow from fundamental physical principles, in particular through the analysis of solutions of the Navier-Stokes equations. Rigorous treatment of turbulence is confronted by several open problems in the field of partial differential equations: the mathematical treatment of boundary layers, the statistical behavior of solutions of the Navier-Stokes equations, the uniqueness of weak solutions to the Euler equations.
Detailed numerical modeling involves equations in three dimensions and it is not yet accessible with modern computers in many practical applications. The turbulence models used in applications are based on ad hoc closures at small scales, leading to a numerical approach called the Large Eddy Simulation.
Singularities in Mathematical Physics
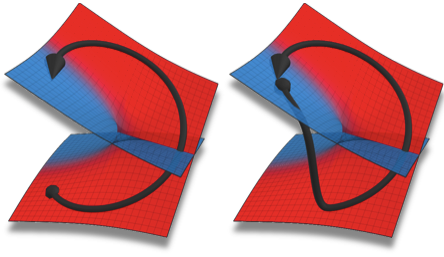 Physical systems with loss or gain have resonant modes that decay or grow exponentially with time. Whenever two such modes coalesce both in their resonant frequency and their rate of decay or growth, an "exceptional point" occurs. Mathematically, this defines a spectral singularity associated with a Jordan block.
Physical systems with loss or gain have resonant modes that decay or grow exponentially with time. Whenever two such modes coalesce both in their resonant frequency and their rate of decay or growth, an "exceptional point" occurs. Mathematically, this defines a spectral singularity associated with a Jordan block.
We study theoretically and experimentally new physical effects in wave dynamics, optics and quantum physics, that arise due to the exceptional points. In a recent experiment [Nature (2016) 537:7618, 76-79], we designed a waveguide structure that steers incoming waves around an exceptional point during the transmission process. In this way, mode transitions are induced that transform this device into a robust and asymmetric switch between different waveguide modes.


